线性数据结构

1、数组

1.1知识点：

数组的优点:

• 存取速度快

数组的缺点:

• 事先必须知道数组的长度
• 插入删除元素很慢
• 空间通常是有限制的
• 需要大块连续的内存块
• 插入删除元素的效率很低

1.2实现一个动态数组

• 由于数组长度时固定的，因此动态数组，在每次新增元素时，需要判断是否需要扩容

public class Array<E>{

    private E [] data;

    //数组的实际个数 第一个没有元素的索引
    private int size;

   public Array(int capacity){
        data = (E[])new Object[capacity];
        size = 0;
    }

    public Array(E[] arr){
       data = (E[])new Object[arr.length];
       for (int i=0;i<arr.length;i++){
           data[i] = arr[i];
           size = arr.length;
       }
    }

    //无参构造函数，默认的数组容量为10
    public Array(){
       this(10);
    }
    //获取数组中的元素个数
    public int getSize(){
       return size;
    }
    //获取数组的中容量
    public int getCapacity(){
       return data.length;
    }

    //判断数组是否为空
    public boolean isEmpty(){
       return size==0;
    }

    //向数组最后添加元素
    public void addLast(E e){
        add(size,e);//相当于调用指定插入（插入最后一个）
    }

    //向数组中第一位置插入元素
    public void addFirst(E e ){
       add(0,e);
    }

    //向数组指定位置插入插入元素
    public void add(int index,E e){
       if(size == data.length){//新增元素时，需要判断当前数组的容量是否够，如果不够会进行扩容
           resize(getCapacity()*2);
       }
       if(index<0||index>size){
           throw new IllegalArgumentException("传入的参数错误");
       }
       for(int i= size-1;i>=index;i--){//从数组元素末尾开始，依次将元素往后移一位
           data[i+1] = data[i];
       }
       data[index] = e;
       size++;
    }
    //对数组进行扩容，新创建一容量大的数组，将原数组 -> 新数组
    public void resize(int newCapacity){
        E[] newDate = (E[]) new Object[newCapacity];
        for(int i=0;i<size;i++){
            newDate[i] = data[i];
        }
        data = newDate;
    }
    //获取index位置的元素
    public E get(int index){
        if(index<0||index>=size){
            throw new IllegalArgumentException("传入的参数错误");
        }
       return data[index];
    }
    public E getFirst(){
        return get(0);
    }
    public E getLast(){
       return get(size-1);
    }
    //修改某个位置的元素
    public void set (int index,E e){
        if(index<0||index>=size){
            throw new IllegalArgumentException("传入的参数错误");
        }
        data[index] = e;
    }

    //查找数组中的元素
    public boolean contains(E e){
       for(int i=0;i<size;i++){
           if(data[i].equals(e)){
               return true;
           }
       }
        return false;
    }
    //查找某个元素位置
    public int find(E e){
        for(int i=0;i<size;i++){
            if(data[i].equals(e)){
                return i;
            }
        }
        return -1;
    }

    //从数组中删除index的元素，返回删除的元素
    public E remove(int index){
        if(index<0||index>=size){
            throw new IllegalArgumentException("传入的参数错误");
        }
       E e = data[index];
       for(int i=index+1;i<size;i++){
           data[i-1] = data[i];
       }
       size--;
       return e;
    }

    public E removefist(){
       return remove(0);
    }
    public E removeLast(){
        return remove(size-1);
    }

    //删除指定元素
    public void reoveElement(E e){
        int index  = find(e);
        if(index !=-1)
            remove(index);
    }
}

2、链表

2.1知识点

链表优点

• 空间没有限制
• 插入删除元素很快

链表缺点 存取速度很慢

2.2分类

• 单向链表 一个节点指向下一个节点。
• 双向链表 一个节点有两个指针域。
• 循环链表 能通过任何一个节点找到其他所有的节点，将两种(双向/单向)链表的最后一个结点指向第一个结点从而实现循环。

2.3实现单链表

• 单链表的头节点有些特殊，在处理删除操作时，头节点，由于没有上一个节点指向它，因此处理时需要特殊处理，为了方便单链表操作，加一个虚拟头结点

public class LinkedList<E> {

    private class Node{
        public E e;
        public Node next;

        public Node(E e,Node next){
            this.e = e;
            this.next = next;
        }
        public Node(E e){
            this(e,null);
        }
        public Node(){
            this(null,null);
        }

        public String toString(){
            return this.e.toString();
        }
    }

    private Node dummyHead;
    private int size;
    
    //初始化链表时，默认头结点元素为空，指向的元素为空
    public LinkedList(){
        dummyHead = new Node(null,null);
        size = 0;
    }
}    

2.3.1插入节点

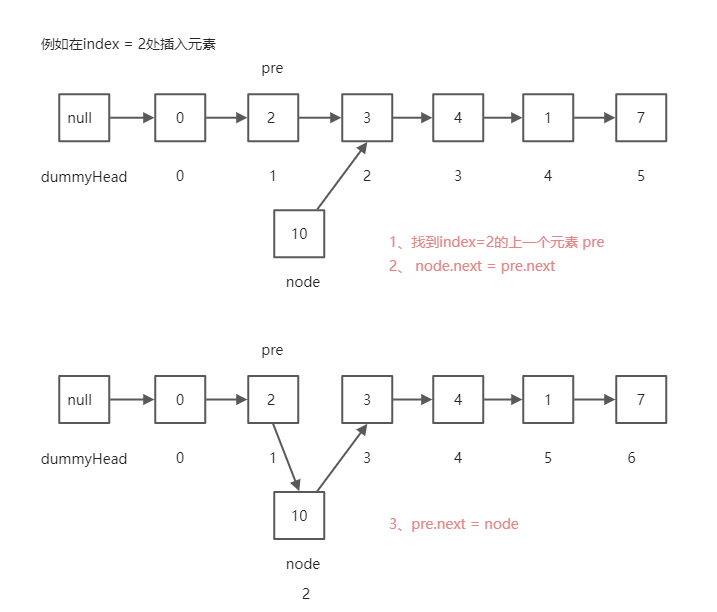
• 例如：在index = 2处插入元素 10

思路

• 关键：找到要添加节点的前一个节点
  • 先找到index=2的前一个元素 pre
  • 元素10的下一个节点指向pre.next
  • pre指向元素10

实现

public void add(int index,E e){
    if(index<0||index>size){//校验 index 是否合法
        throw new IllegalArgumentException("传入参数错误");
    }
    Node prev = dummyHead;
    for(int i=0;i<index;i++){
        prev = prev.next;//遍历找到 pre
    }
    Node node = new Node(e);
    node.next = prev.next;
    prev.next = node;
    size++;
} 
//在链表头添加元素e
public void addFirst(E e){
        add(0,e);
}
//在链表末尾添加元素e
public void addLast(E e){
        add(size,e);
}

2.3.2删除节点

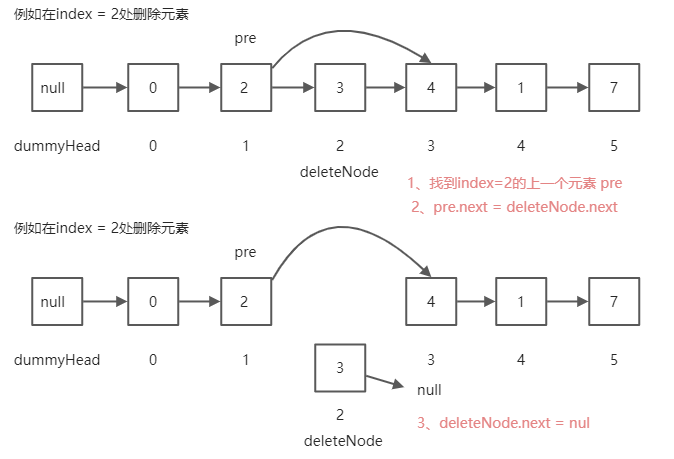
• 例如：删除index=2的元素

思路：

找到index=2的上一个元素 pre

pre.next = 删除元素.next

删除元素.next = null

实现

//从链表中删除index的元素
public E remove(int index){
    if(index<0||index>=size){
        throw new IllegalArgumentException("传入参数错误");
    }
    Node prev = dummyHead;
    for(int i=0;i<index;i++){
        prev = prev.next;//遍历找到 pre
    }
    Node retNode = prev.next;//先暂存 要删除的node
    prev.next = retNode.next;
    retNode.next = null; 
    size--;
    return retNode.e;
}
//删除第一个元素
public E removeFirst(){
     return remove(0);
}

2.3.3查找节点

同之前删除，增加时找pre节点的逻辑，但是这里是找pre.next

//获取链表第index位置的元素
public E get(int index){
    if(index<0||index>=size){
        throw new IllegalArgumentException("传入参数错误");
    }
    Node cur = dummyHead.next;
    for(int i=0;i<index;i++){
        cur = cur.next;
    }
    return cur.e;
}

//查找链表中是否有元素e
public boolean contains(E e){
    Node cur = dummyHead.next;
    while (cur!=null){
        if(cur.e.equals(e)){
            return true;
        }else {
            cur = cur.next;
        }
    }
    return false;
}

2.3.4其它操作

• 获取链表大小

public int getSize(){
    return size;
}

• 判断链表是否为空

public boolean isEmpty(){
    return size==0;
}

2.3.5小优化

新增删除操作，都有一个寻找index的前驱节点的操作，可以单独把该方法抽取出来，参考双链表实现

2.4实现双向链表

双向链表(双链表)是链表的一种。和单链表一样，双链表也是由节点组成，它的每个数据结点中都有两个指针，分别指向直接后继和直接前驱。所以，从双向链表中的任意一个结点开始，都可以很方便地访问它的前驱结点和后继结点。一般我们都构造双向循环链表。

• 表头为空，表头的后继节点为节点“0”，节点“4”的后继的节点为表头

2.4.1双链表的基础操作

• 构造函数、获取链表大小、判断链表是否为空

public class DoubleLink<T> {

    // 表头
    private DNode<T> dummyHead;
    // 节点个数
    private int size;

    // 双向链表“节点”对应的结构体
    private class DNode<T> {
        public DNode prev;
        public DNode next;
        public T value;

        public DNode(T value, DNode prev, DNode next) {
            this.value = value;
            this.prev = prev;
            this.next = next;
        }
    }
    //构造函数
    public DoubleLink(){
      dummyHead = new DNode<>(null,null,null);//初始化时，表头没有数据
      dummyHead.prev = dummyHead.next = dummyHead;
      size = 0;
  }
}    

• 获取链表第index位置的节点

//获取第index位置的元素
private DNode<T> getNode(int index){
    if(index<0||index>size){
        throw new IllegalArgumentException("传入参数错误");
    }
    int mid = size/2;
    //正向查找
    if(index<mid){
        DNode dNode = dummyHead.next;
        for (int i=0;i<index;i++){
            dNode = dNode.next;
        }
        return dNode;
    }
    //反向查找
    DNode dNode = dummyHead.prev;
    for(int i=0;i<(size-index-1);i++){
        dNode = dNode.prev;
    }
    return dNode;
        //获取第index节点的值
    public T get(int index){
        return getNode(index).value;
    }

    //获取第一个节点的值
    public T getFirst(){
        return getNode(0).value;
    }
    //获取最后一个节点的值
    public T getLast(){
        return getNode(size-1).value
    }

}

2.4.2双链表删除节点

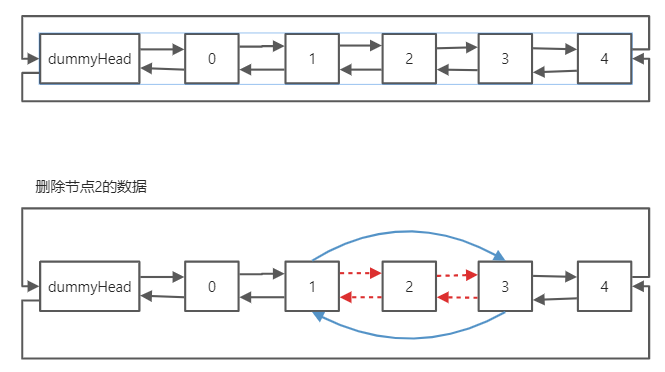
• 删除第index=2位置的节点
• 思路:
  • 找到index位置的前驱1和后继3
  • 修改前驱1的后继为3
  • 修改后继3的前驱为1
• 实现

//删除第index位置元素
public void remove(int index){
    DNode inode = getNode(index); //获取index位置的元素
    DNode preNode = inode.prev;  //获取index位置前驱
    DNode nextNode = inode.next;//获取index位置的后继
    preNode.next = nextNode;
    nextNode.prev = preNode;
    inode=null;
    size--;
}
//删除第一个节点
public void removeFirst(){
    remove(0);
}
//删除最后一个节点
public void removeLast(){
    remove(size-1);
}

2.4.3双链表添加节点

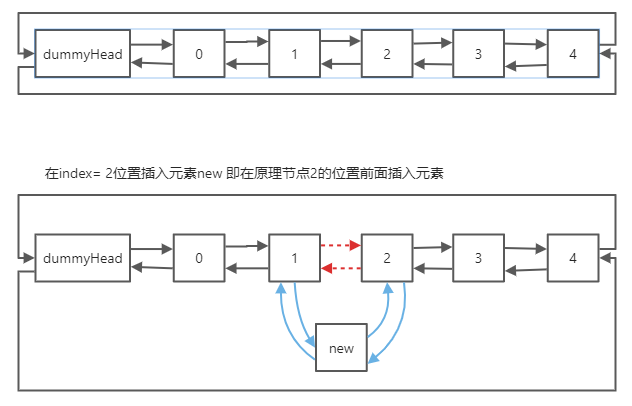
• 在index=2位置添加元素
• 思路
  • 找到index位置的元素2，新节点在2的前面插入
  • 让new的后继指向2，前驱指向1
  • 让1的后继指向new 2的前驱指向new
  • 注意：插入第一个元素和末尾元素的特殊情况，因为它们的相邻节点为dummyHead，根据dummyHead的特殊性插入。可避免size=0的特殊情况

//在index位置插入元素
public void add(int index, T t){
    if(index==0){//index=0时，需要特殊处理，因为此时 0 的前驱为dummyHead 测试发现  这里不特殊处理也行
        DNode newNode = new DNode<>(t,dummyHead,dummyHead.next);
        dummyHead.next.prev = newNode;//先把原 dummyHead的后继的前驱指向 new
        dummyHead.next = newNode;//再把dummyHead.next 指向 new
        size++;
        return;
    }
    DNode iNode = getNode(index);
    DNode newNode = new DNode<>(t,iNode.prev,iNode);
    DNode pre = iNode.prev;
    pre.next =newNode;
    iNode.prev = newNode;
    size++;
}
//插入第一个元素
public void addFirst(T t){
    add(0,t);
}
//插入最后一个元素 
// 注意：这里不可以直接调用 add(int index, T t)方法，测试发现，这里只能这样写，因为当size = 0 时，index会无效
public void addLast(T t){
    DNode newNode = new DNode<>(t,dummyHead.prev,dummyHead);
    dummyHead.prev.next = newNode;
    dummyHead.prev = newNode;
    size++;
}

2.4.4遍历链表

@Override
public String toString(){
    StringBuilder stringBuilder = new StringBuilder();
    DNode dNode = dummyHead.next;
    while (dNode.value!=null){
        stringBuilder.append(dNode.value);
        stringBuilder.append("==>");
        dNode = dNode.next;
    }
    return stringBuilder.toString();
}

3、栈

3.1知识点

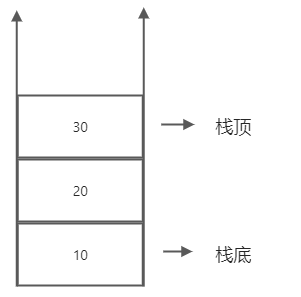
• 栈（stack），是一种线性存储结构，它有以下几个特点：

  • 栈中数据是按照"后进先出（LIFO, Last In First Out）"方式进出栈的。
  • 向栈中添加/删除数据时，只能从栈顶进行操作。

• 栈通常包括的三种操作：push、peek、pop。

  • push -- 向栈中添加元素。
  • peek -- 返回栈顶元素。
  • pop -- 返回并删除栈顶元素的操作。

• 栈的示意图

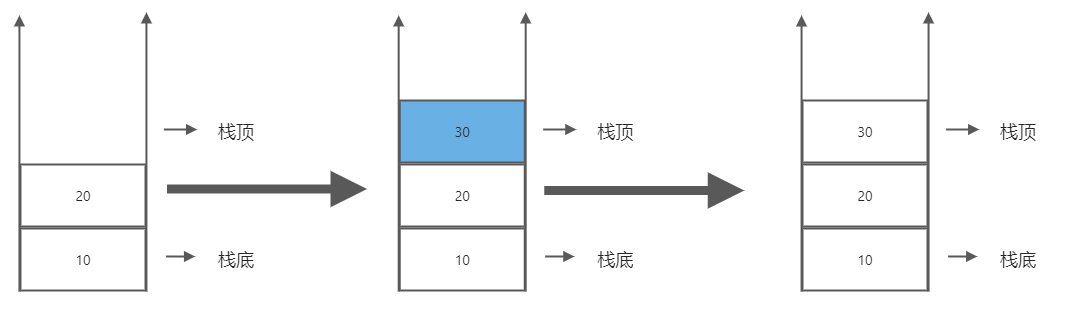
• 出栈

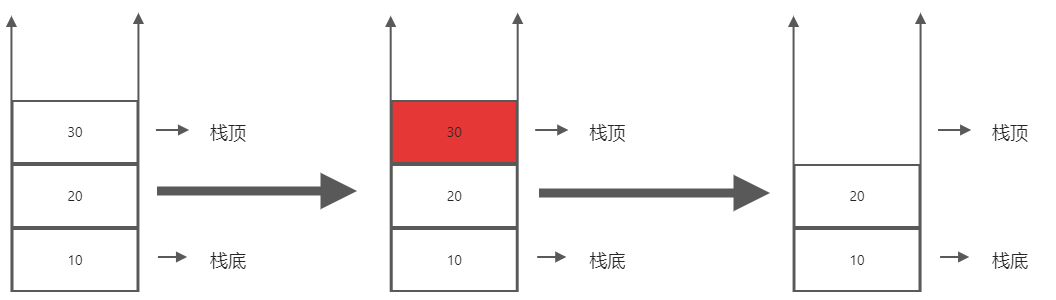
• 入栈

3.2实现栈

3.2.1数组实现栈

• 用我们之前的实现的动态数组，很容易实现栈

public class ArrayStatck<E>  implements Statck<E>{
    Array<E> array;
    public ArrayStatck(int capacity){
        array = new Array<>(capacity);
    }
    public ArrayStatck(){
        array = new Array<>();
    }
    @Override
    //查看栈一共多少个元素
    public int getSize() {
        return array.getSize();
    }

    @Override
    //判断栈是否为空
    public boolean isEmpty() {
        return array.isEmpty();
    }

    public int getCapacity(){
        return array.getCapacity();
    }

    @Override
    //向栈中添加一个元素 入栈
    //由于栈是 后进先出的原则，因此在添加元素时，相当于数组的 addLast方法
    public void push(E e) {
        array.addLast(e);
    }

    @Override
    //从栈中拿出栈顶的元素  出栈
    public E pop() {
        return array.removeLast();
    }

    @Override
    //看栈顶的元素是谁
    public E peek() {
        return array.getLast();
    }

    public String toString(){
        StringBuilder res  = new StringBuilder();
        res.append("Stack: ");
        res.append("[");
        for(int i=0;i<array.getSize();i++){
            res.append(array.get(i));
            if(i!=array.getSize()-1){
                res.append(",");
            }
        }
        res.append("] top");
        return res.toString();
    }
}

3.2.2链表实现栈

• 这里用双链表实现栈

public class DoubleLinkStatic<E> implements Statck<E> {
    private DoubleLink doubleLink;

    public DoubleLinkStatic(){
        doubleLink = new DoubleLink<>();
    }

    @Override
    public int getSize() {
        return doubleLink.getSize();
    }

    @Override
    public boolean isEmpty() {
        return doubleLink.isEmpty();
    }

    @Override
    public void push(E e) {
        doubleLink.addLast(e);
    }

    @Override
    public E pop() {
        E e = (E) doubleLink.getLast();
        doubleLink.removeLast();
        return e;
    }

    @Override
    public E peek() {
        E e = (E) doubleLink.getLast();
        return e;
    }
    @Override
    public String toString(){
        return doubleLink.toString();
    }
}

4、队列

4.1知识点

• 队列（Queue），是一种线性存储结构。它有以下几个特点：

  • 队列中数据是按照"先进先出（FIFO, First-In-First-Out）"方式进出队列的。
  • 队列只允许在"队首"进行删除操作，而在"队尾"进行插入操作。

• 队列通常包括的两种操作：入队列 和 出队列。

• 队列示意图

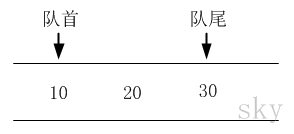
• 出队

• 入队

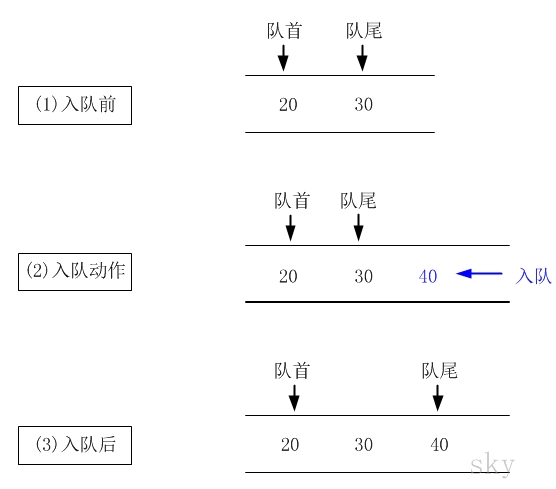
4.2实现队列

4.2.1数组实现队列

public class ArrayQueue <E> implements Queue<E>{


    private Array<E> arrayE;

    public ArrayQueue(int capacity){
        arrayE = new Array<>(capacity);
    }
    public ArrayQueue(){
        arrayE = new Array<>();
    }

    @Override
    public int getSize() {
        return arrayE.getSize();
    }

    @Override
    public boolean isEmpty() {
        return arrayE.isEmpty();
    }

    @Override
    //像队列添加元素  在末尾添加
    public void enque(E e) {
        arrayE.addLast(e);
    }

    @Override
    //从队列中拿出元素  在头拿出
    public E dequeue() {
        return arrayE.removefist();
    }

    @Override
    //查看队首是谁
    public E getFront() {
        return arrayE.getFirst();
    }

    @Override
    public String toString(){
        StringBuilder res  = new StringBuilder();
        res.append("Queue: ");
        res.append("front [");
        for(int i=0;i<arrayE.getSize();i++){
            res.append(arrayE.get(i));
            if(i!=arrayE.getSize()-1){
                res.append(",");
            }
        }
        res.append("] tail");
        return res.toString();
    }
}

4.2.2链表实现队列

• 这里用双链表实现

public class DoubleLinkQueue <E> implements Queue<E>{

    private DoubleLink doubleLink;

    public DoubleLinkQueue(){
        doubleLink = new DoubleLink();
    }

    @Override
    public int getSize() {
        return doubleLink.getSize();
    }

    @Override
    public boolean isEmpty() {
        return doubleLink.isEmpty();
    }

    @Override
    public void enque(E e) {//入队
        doubleLink.addLast(e);
    }

    @Override
    public E dequeue() {//出队
        E e = (E) doubleLink.getFirst();
        doubleLink.removeFirst();
        return e;
    }

    @Override
    public E getFront() {//获取堆首元素
        E e = (E) doubleLink.getFirst();
        return e;
    }
    @Override
    public String toString(){
        StringBuilder res  = new StringBuilder();
        res.append("Queue: ");
        res.append("front [");
        res.append(doubleLink.toString());
        res.append("] tail");
        return res.toString();
    }
}

参考

• https://class.imooc.com/sale/datastructure?mc_marking=847f8fb5de6faa3343df639065d45b7d&mc_channel=imoocsearch
• http://www.cnblogs.com/skywang12345/p/3561803.html