归并排序(Merge Sort)
2022年5月19日
归并排序(Merge Sort)
基本思想
分解:将当前区间一分为二,即求分裂点mid = (l+r)/2
求解:递归对两个子区间arr[l,mid]、arr[mid+1,r]进行排序。递归的终止条件子区间(长度为1)l>=r
合并:将已经排序的两个子区间arr[l,mid]、arr[mid+1,r]合并
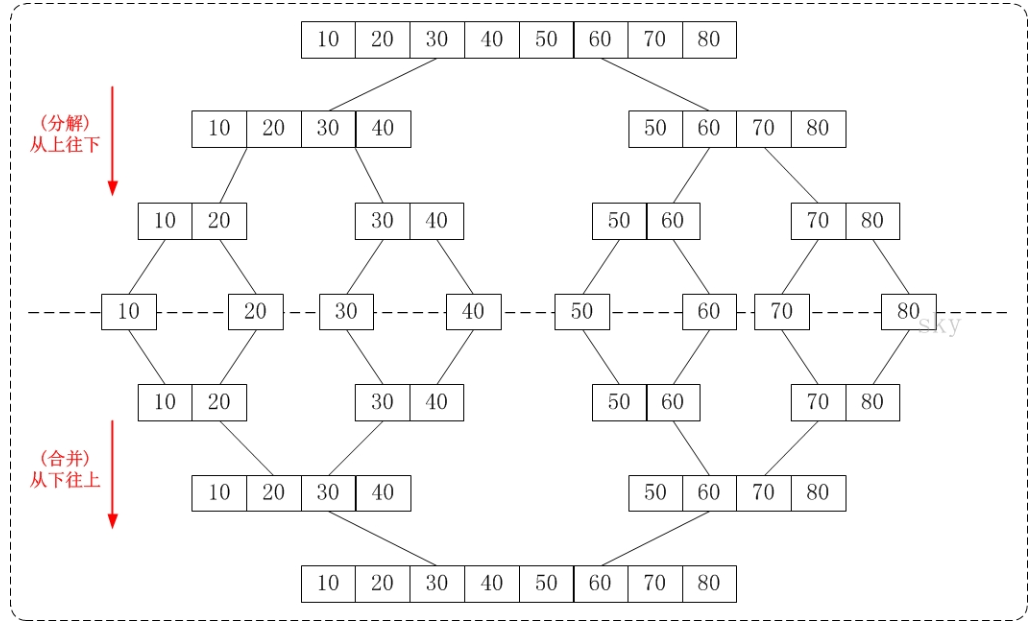
其中分解和求解很好理解。
合并的思路:
- 首先需要copy一份arr[l,r]->temp[]
- 在temp[]中对应位置,分别找arr[l,mid]和arr[mid+1,r]中最小的元素,然后进行比较,取出最小值,放到arr[l,r]中
- 注意越界问题
- arr[l,mid]遍历结束了,剩下的直接取arr[mid+1,r]中即可
- arr[mid+1,r]遍历结束了,剩下的直接取arr[l,mid]即可

代码实现
public static <E extends Comparable> void sort(E [] arr){
sort(arr,0, arr.length-1);
}
private static <E extends Comparable> void sort(E[] arr,int l,int r){
if(l>=r){
return;
}
int mid = (l+r)/2;
sort(arr,l,mid);//对前半段排序
sort(arr,mid+1,r);//对后半段排序
merge(arr,l,mid,r);//对前后两端 和并
}
//合并两个有序数组区间 arr[l,mid] arr[mid+1,r]
private static <E extends Comparable> void merge(E[] arr, int l, int mid, int r) {
E[] temp = Arrays.copyOfRange(arr, l, r + 1);//这个复制的方法是前闭后开,因此时间copy的数组为[l,r]
int i = l;
int j = mid + 1;
for (int k = l; k <= r; k++) {
//首先判断越界的情况,即i跑到了mid的右边
if (i > mid) {
//这里取temp[j-1]原因是,temp是copy得来,但是它的下标是从0开始的。arr是从l开始的。
//因此也就是temp[0]对应arr[l],temp[1]对应arr[l+1],也就是它们存在下标偏移量(1)
arr[k] = temp[j - l];
j++;
} else if (j > r) {//j跑到r的右边,即右边的都遍历完了(右边的都比左边的小),因此此时取左边的
arr[k] = temp[i - l];
i++;
} else if (temp[i - l].compareTo(temp[j - l]) <= 0) {//如果都没有越界,才进行比较
arr[k] = temp[i - l];
i++;
} else {
arr[k] = temp[j - l];
j++;
}
}
}
归并排序复杂度
O(nlogn)
