红黑树(R-B Tree)
红黑树(R-B Tree)
R-B Tree,全称是Red-Black Tree,又称为“红黑树”,它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
R-B Tree简介
红黑树的特性
- 每个节点是黑色或者红色。
- 根节点是黑色。
- 每个叶子节点都是黑色(指向空的叶子节点)。
- 如果一个叶子节点是红色,那么其子节点必须都是黑色的。
- 从一个节点到该节点的子孙节点所有路径上包含相同数目的黑节点。
2-3树
红黑树与2-3树具有等价性,我们在了解红黑树前先了解2-3树对我们理解红黑树是有帮助的,同时,对于理解B树也是有帮助的(用于磁盘存储,文件系统或数据库存储)
2-3树特性
满足二分搜索树的基本性质
是一颗绝对平衡的树
节点可以存放一个或者两个元素
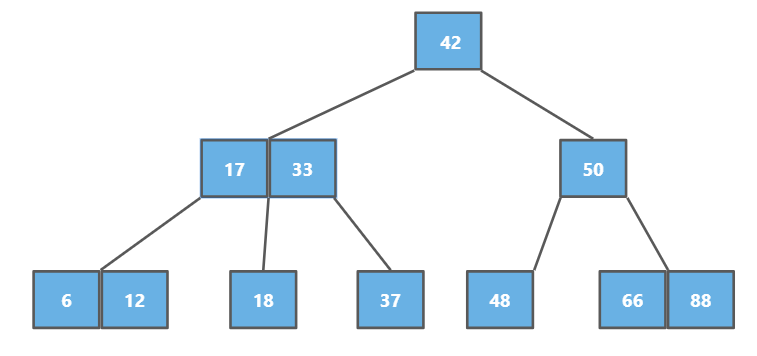
上图是一个2-3树,满足二分搜索树的基本性质,比如根节点42的左子树全部比根节点小;42的左孩子是一个3节点,具有两个元素 [17 33] ,并且左孩子都小于17,右孩子大于33,中孩子大于17且小于33;根节点的右孩子是一个二节点,只有一个元素 50,并且有两个孩子。
2-3数新增元素
2-3树是一个绝对平衡的树,那么它在新增元素时是如何维护平衡性的?
下面以各种添加案例来说明

2-3树添加节点,永远不会添加到一个空的位置 因此37添加到42左边 融合为三节点
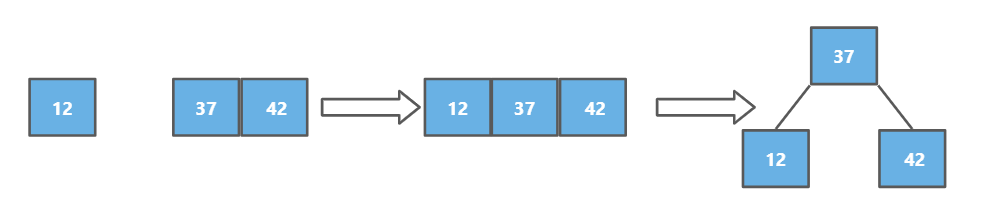
先融合为四节点,但是2-3树不能存在4节点,所以此时的根节点可以分裂成一棵子树,有三个2-节点组成的绝对平衡树
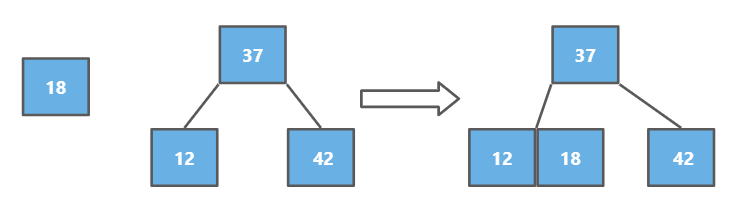
同理18添加到12的右边即可
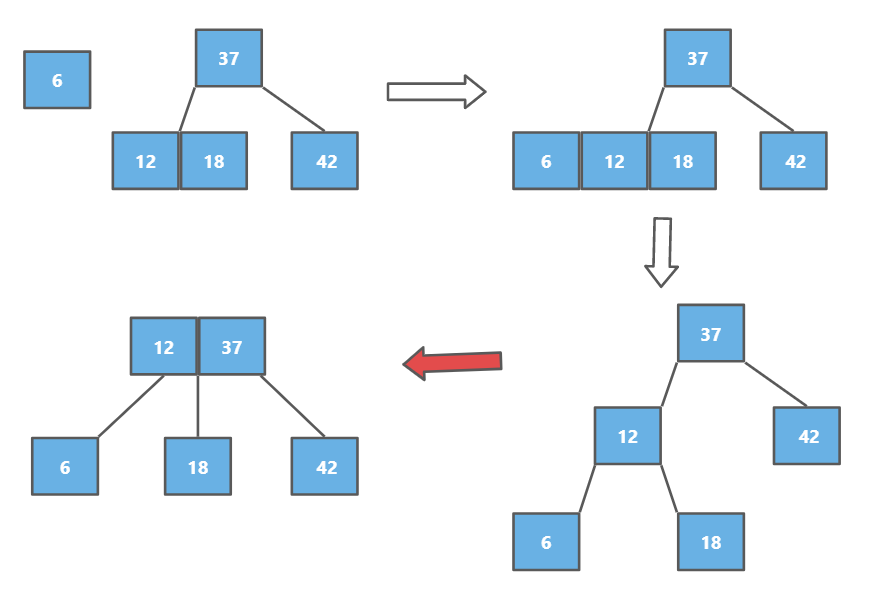
先添加到12的左侧,然后对四节点拆解,但是此时2-3树就不是绝对平衡的树,因此让12和父亲节点融合
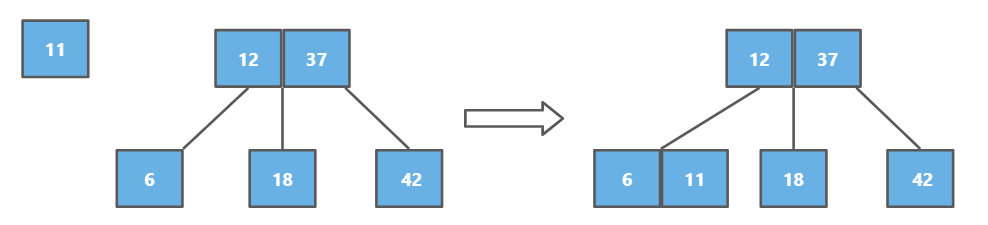
同理放到6的右侧
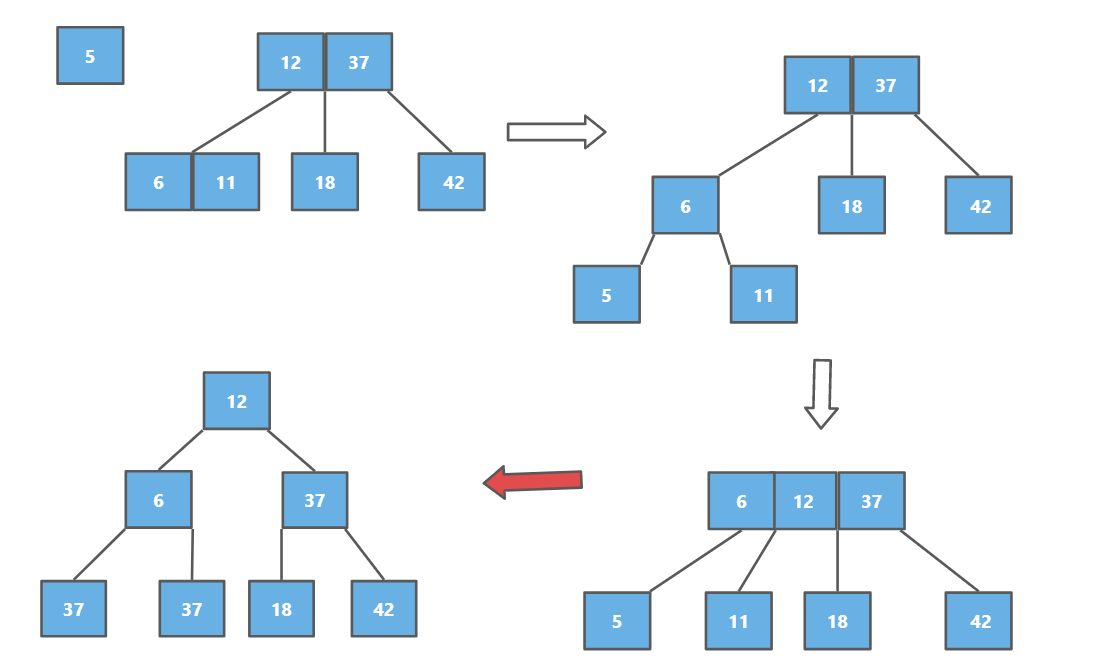
添加的5节点为3节点,并且父亲节点也是三节点,会进行两次拆解
红黑树与2-3树的等价性
如何等价的?
对于红黑树,它只能存在一个元素,所以2-3树中2节点和3节点在红黑树中对应关系
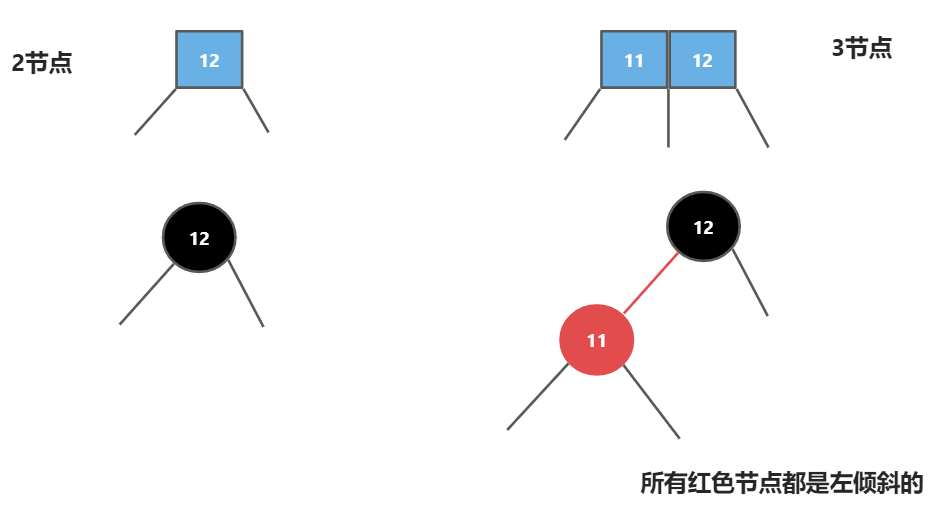
也就是11节点和12节点在原2-3树中,是在同一层
初始化node节点
private static final boolean Red = true;
private static final boolean Black = false;
class Node{
private Node left; //左孩子
private Node right; //右孩子
private E e; //值
public boolean color;
public Node(E e){
left = null;
right = null;
this.e = e;
color = Red;//新增节点默认是红色
}
}
判断一个节点是否是红色
如果一个节点是空,定义为黑节点,因为红色节点的含义,就是表示和父亲节点组合成 2-3节点的3节点,因此空节点,谈不上融合3节点,因此这里为黑节点
private boolean isRed(Node node){
if (node==null){
return Black;//
}
return node.color;
}
再看红黑树5个性质
- 每个节点是黑色或者红色。
- 根节点是黑色。
- 每个叶子节点都是黑色(指向空的叶子节点)。
- 如果一个叶子节点是红色,那么其子节点必须都是黑色的。
- 从一个节点到该节点的子孙节点所有路径上包含相同数目的黑节点。
1、第一点很好理解
2、对比2-3树,红色节点本身的意义就是和父亲节点在同一层,因此根节点一点不可能是红色,因为其没有父亲节点,只能是黑色。
3、第三条我们要看清楚是指的最后的空节点,这条与其说是性质,不如说是定义,我们再红黑树定义空为黑色。
4、红色节点下面有两个节点,如果子节点是2-节点的话,那肯定就是黑色,如果是3-节点,那首先连接的也是黑色,然后黑色的左节点才是红色(而对于黑色节点,它的右孩子肯定是黑色,左孩子就不一定了)
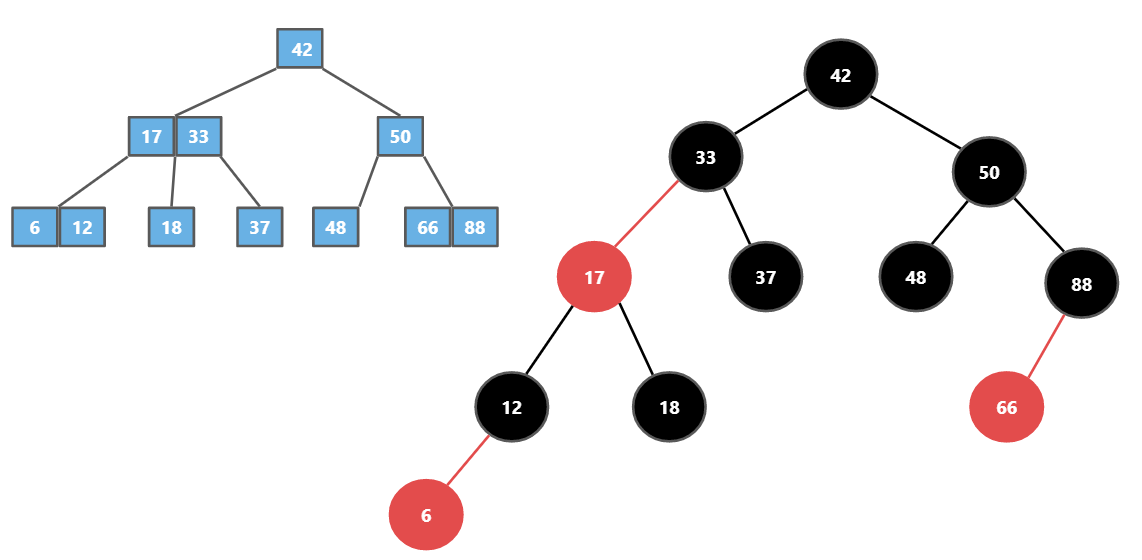
5、这条是核心,我们看下下面的图就一清二楚了
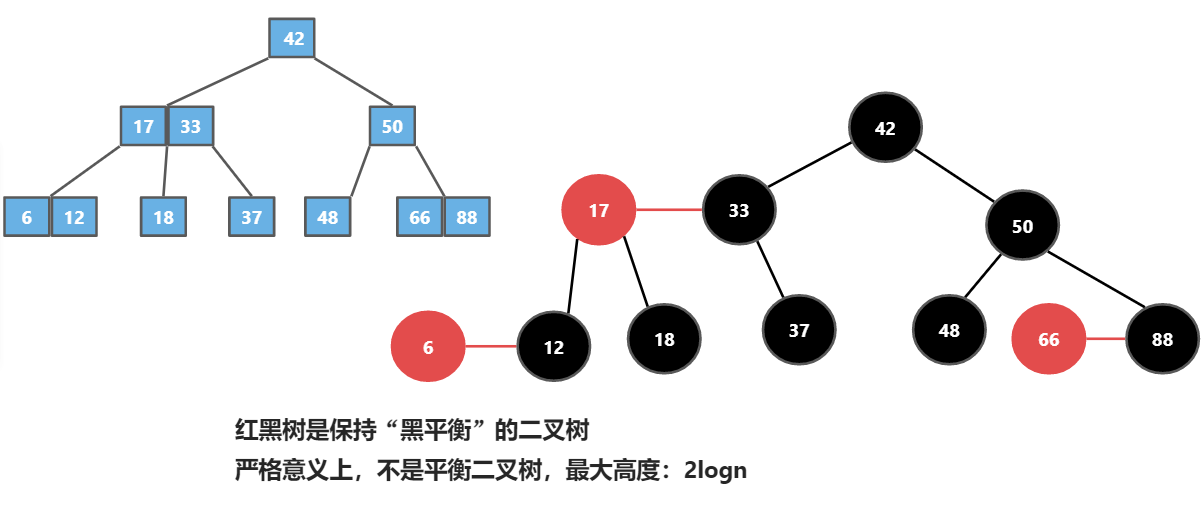
由于红黑树的最大高度为2logn,它会比AVL树的高度高,所以我们在红黑树上对元素的寻找会比AVL慢一点,虽然都是O(logn)级别,但是为什么红黑树这么重要,因为对于红黑树来说,添加与删除元素这两个操作相比于AVL来说更快一些,如果我们存储的数据结构要经常发生添加和删除的变动的话,相应的使用红黑树会更好些。而数据不怎么变动,查询更多的话,AVL还是快一点点。
红黑树添加元素
最终的根节点是黑色
public void add(E e) {
root = add(root, e);
root.color = Black;//最终的根节点是黑色
}
左旋转
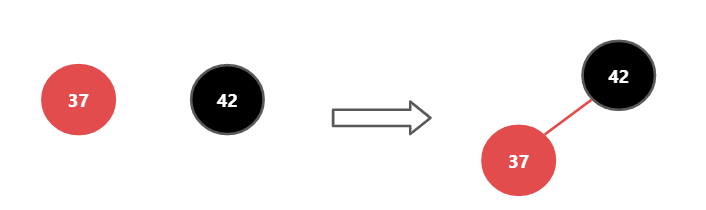
插入红色节点 37,即如果往一个黑色元素左侧添加时,那么直接添加一个红色的就好了
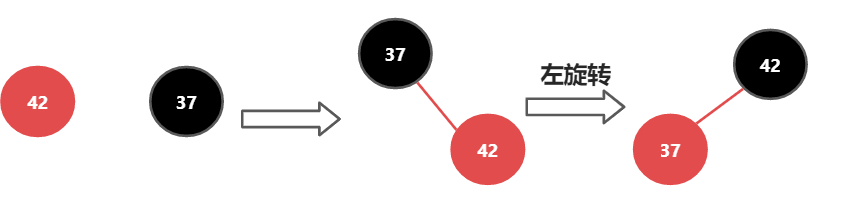
但是如果加入的元素在黑色元素的右侧,则需要进行左旋转
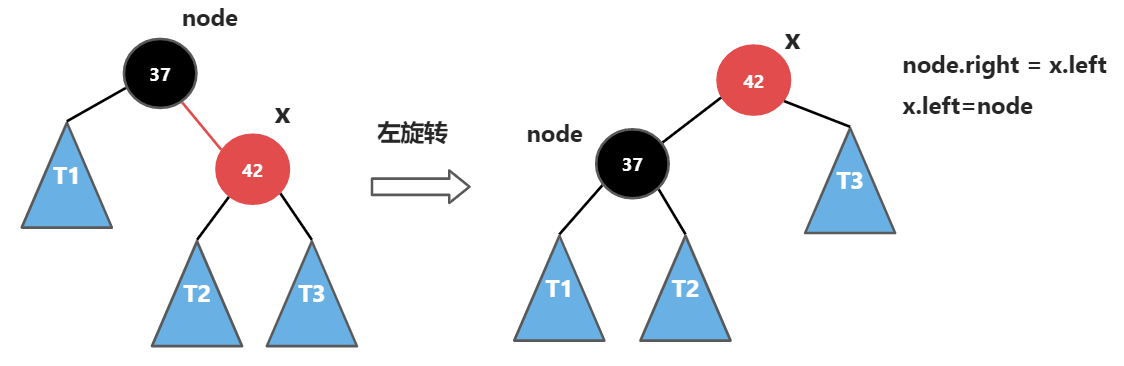
左旋转和AVL树的规则相同
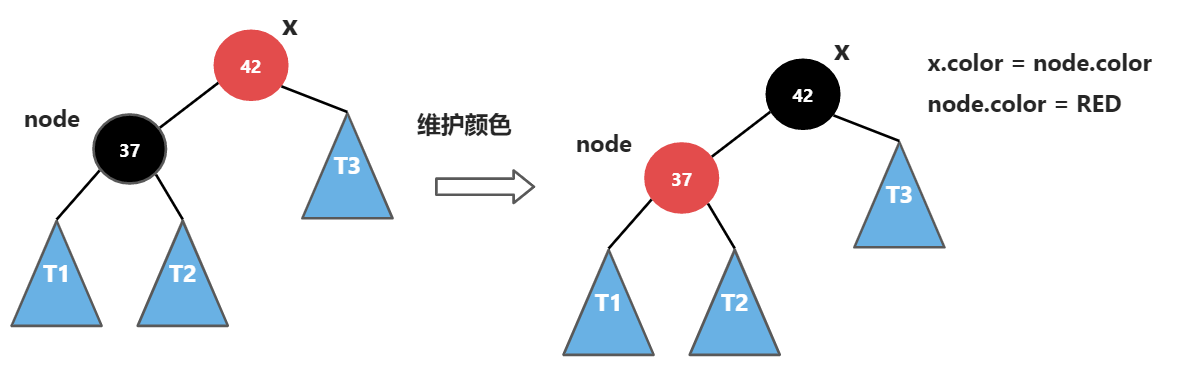
在左旋转的基础上,还需要做维护颜色的操作
注:x.color node.color 可能导致x的节点也是红色,37节点也是红色,但是这里本身是一个递归子过程,x还会传回去,还会有后续处理 即旋转并不维持红黑树的性质,仅维护37和42是一个正确的三节点,即37 需要是47的左子树
代码
// node x
// / \ / \
// T1 x ---------> node T3
// / \ / \
// T2 T3 T1 T2
private Node LeftRotate(Node node){//以node为根的左旋转,返回旋转后新的根节点
Node x = node.right;
//左旋转
node.right=x.left;
x.left = node;
//维护颜色
x.color = node.color;
node.color = Red;
return x;
}
颜色反转和右旋转
颜色反转
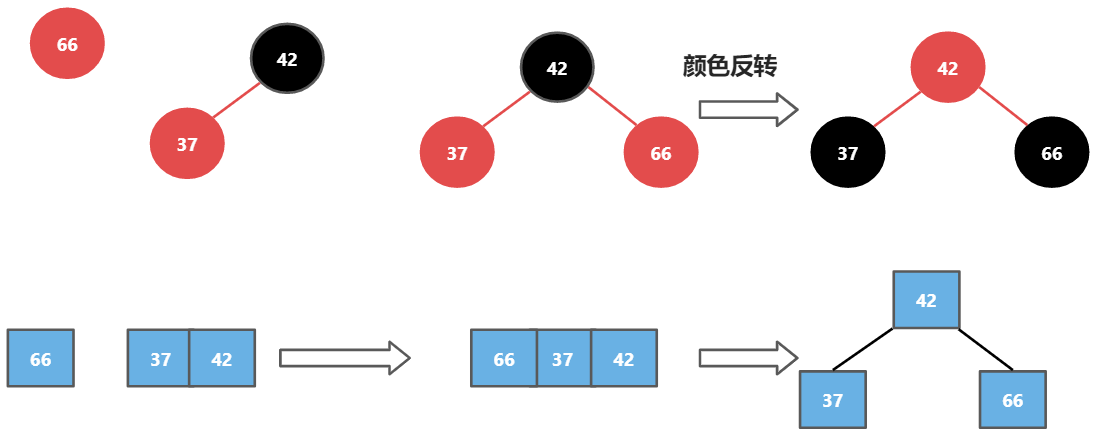
对照2-3树的添加操作,这一步就很好理解了,即先添加为4节点,然后再拆解,而这个拆解过程,对应红黑树中为颜色反转
//颜色反转
private void flipColors(Node node){
node.color = Red;
node.left.color = Black;
node.right.color = Black;
}
右旋转
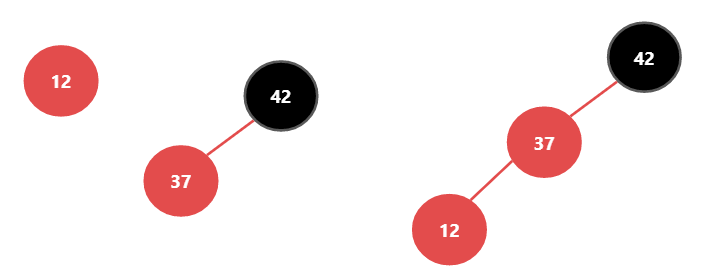
这种情况,需要先对42进行右旋转,再进行颜色反转,步骤请看下图
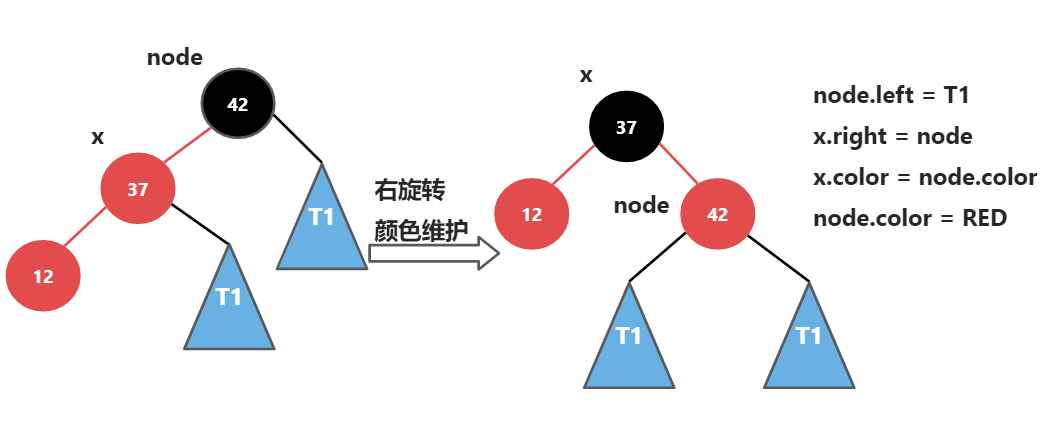
完成右旋转和颜色维护
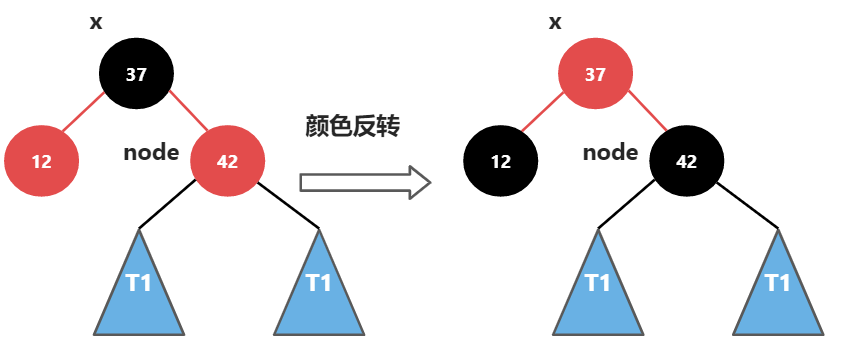
完成颜色反转
private Node rightRotate(Node node){//右旋转
Node x = node.left;
//右旋转
node.left = x.right;
x.right = node;
//维护颜色
x.color = node.color;
node.color = Red;
return x;
}
第三种情况
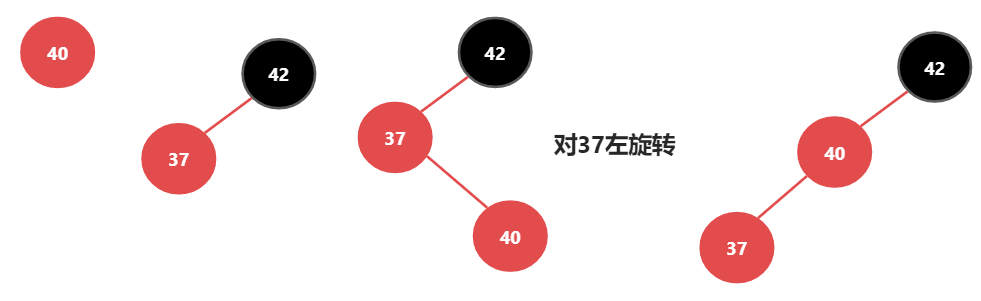
即添加的节点在37的右侧,则先对37进行左旋转,之后就又和之前的情况一样了。
添加代码
然后我们以这个最复杂的案例演示
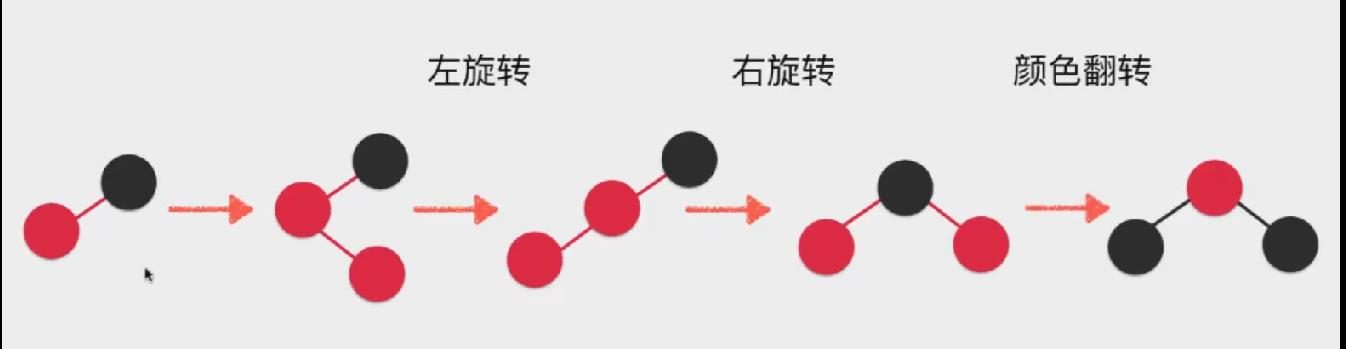
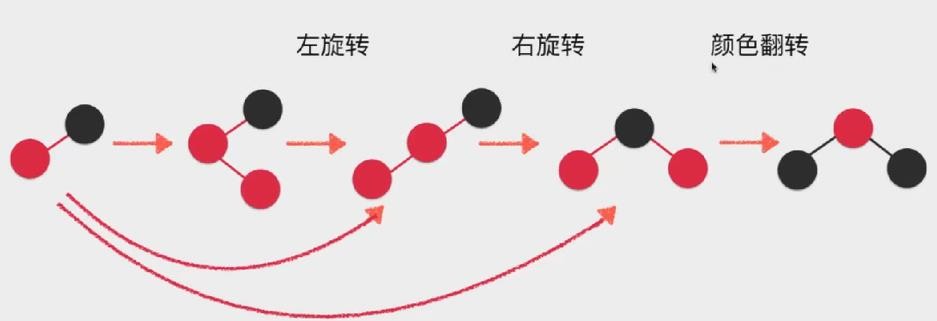
发现在解决最复杂的情况时,都能包含之前解决的情况,因此我们只需要通过if判断,从最复杂逻辑开始处理即可。左旋转->右旋转->颜色翻转
public void add(E e) {
root = add(root, e);
root.color = Black;//最终的根节点是黑色
}
//以node为根的红黑树中插入元素e,递归算法
//返回插入新节点后红黑树的根
public Node add(Node node, E e) {
if (node == null) {
size++;
return new Node(e);
}
if (e.compareTo(node.e) < 0) {
node.left = add(node.left, e);
}
if (e.compareTo(node.e) > 0) {
node.right = add(node.right, e);
}else {//修改当前的值
node.e = e;
}
//维护红黑树的性质
if(isRed(node.right)&&!isRed(node.left)){//右孩子红色,左孩子不是红色
node = LeftRotate(node);
}
if(isRed(node.left)&&isRed(node.left.left)){//左孩子红色,左孩子的左孩子也是红色
node = rightRotate(node);
}
if(isRed(node.left)&&isRed(node.right)){//左右都是红色
flipColors(node);//颜色翻转
}
return node;
}
总结
- 对于完全随机的数据,普通的二分搜索树很好用!
- 缺点:极端情况退化成链表(或者高度不平衡)
- 对于查询较多的使用情况,AVL树很好用!
- 红黑树牺牲了平衡性(21ogn的高度)
- 统计性能更优(综合增删改查所有的操作)
代码
public class RedBlackTree<E extends Comparable<E>>{
private static final boolean Red = true;
private static final boolean Black = false;
class Node{
private Node left; //左孩子
private Node right; //右孩子
private E e; //值
public boolean color;
public Node(E e){
left = null;
right = null;
this.e = e;
color = Red;//新增节点默认是红色
}
}
private Node root;
private int size;
public int size(){
return size;
}
//判断一个节点是否是红色
private boolean isRed(Node node){
if (node==null){
//如果一个节点是空,定义为黑节点,
//因为红色节点的含义,就是表示和父亲节点组合成 2-3节点的3节点
//因此空节点,谈不上融合3节点,因此这里为黑节点
return Black;
}
return node.color;
}
public void add(E e) {
root = add(root, e);
root.color = Black;//最终的根节点是黑色
}
//以node为根的红黑树中插入元素e,递归算法
//返回插入新节点后红黑树的根
public Node add(Node node, E e) {
if (node == null) {
size++;
return new Node(e);
}
if (e.compareTo(node.e) < 0) {
node.left = add(node.left, e);
}
if (e.compareTo(node.e) > 0) {
node.right = add(node.right, e);
}else {//修改当前的值
node.e = e;
}
//维护红黑树的性质
if(isRed(node.right)&&!isRed(node.left)){//右孩子红色,左孩子不是红色
node = LeftRotate(node);
}
if(isRed(node.left)&&isRed(node.left.left)){//左孩子红色,左孩子的左孩子也是红色
node = rightRotate(node);
}
if(isRed(node.left)&&isRed(node.right)){//左右都是红色
flipColors(node);//颜色翻转
}
return node;
}
// node x
// / \ / \
// T1 x ---------> node T3
// / \ / \
// T2 T3 T1 T2
private Node LeftRotate(Node node){//以node为根的左旋转,返回旋转后新的根节点
Node x = node.right;
//左旋转
node.right=x.left;
x.left = node;
//维护颜色
x.color = node.color;
node.color = Red;
return x;
}
private Node rightRotate(Node node){//右旋转
Node x = node.left;
//右旋转
node.left = x.right;
x.right = node;
//维护颜色
x.color = node.color;
node.color = Red;
return x;
}
//颜色反转
private void flipColors(Node node){
node.color = Red;
node.left.color = Black;
node.right.color = Black;
}
@Override
public String toString(){
StringBuilder res = new StringBuilder();
generateBSTString(root, 0, res);
return res.toString();
}
private void generateBSTString(Node node, int depth, StringBuilder res){
if(node == null){
res.append(generateDepthString(depth) + "null\n");
return;
}
res.append(generateDepthString(depth) + node.e +"\n");
generateBSTString(node.left, depth + 1, res);
generateBSTString(node.right, depth + 1, res);
}
private String generateDepthString(int depth){
StringBuilder res = new StringBuilder();
for(int i = 0 ; i < depth ; i ++)
res.append("--");
return res.toString();
}
}
