二叉搜索树

1、简介

二叉查找树(Binary Search Tree)，又被称为二叉搜索树。 它是特殊的二叉树：对于二叉树，假设x为二叉树中的任意一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。那么，这棵树就是二叉查找树。如下图所示：

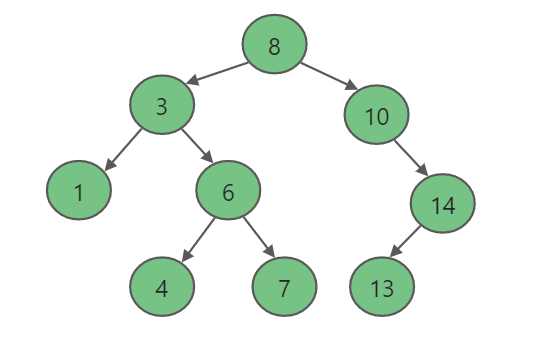
在二叉查找树中：

• 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 任意节点的左、右子树也分别为二叉查找树。
• 没有键值相等的节点（no duplicate nodes）。

2、实现

2.1节点定义

class BSTNode{
    private BSTNode left; //左孩子
    private BSTNode right; //右孩子
    private E e; //值

    public BSTNode(E e){
        left = null;
        right = null;
        this.e = e;
    }
}

2.2遍历

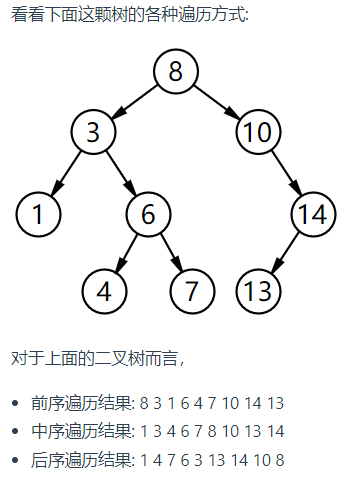
前序遍历

//前序遍历
public void preOrder(){
    preOrder(root);
}
public void preOrder(BSTNode node){
    if (node!=null){
        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }
}

中序遍历

//中序遍历
public void inOrder(){
    inOrder(root);
}
public void inOrder(BSTNode node){
    if (node!=null){
        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }
}

后续遍历

//后续遍历
public void postOrder(){
    postOrder(root);
}
public void postOrder(BSTNode node){
    if (node!=null){
        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.e);
    }
}

2.3查找元素

查找是否存在元素

//判断是否有元素e
public boolean contains(E e){
    return contains(root,e);
}

//判断以node为根节点的二分搜索树，是否有e
private boolean contains(BSTNode node, E e) {
    if (node == null) {
        return false;
    }
    if (e.compareTo(node.e) == 0) {
        return true;
    } else if (e.compareTo(node.e) > 0) {
        return contains(node.right, e);
    } else {
        return contains(node.left, e);
    }
}

2.4最大值&最小值

最大值

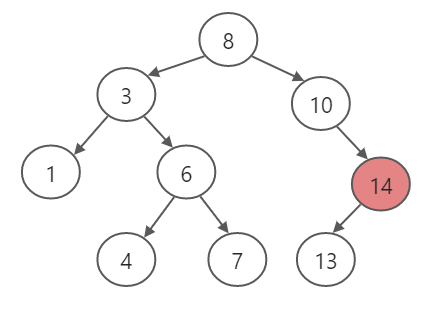
实现思路：

• 递归找右孩子
• 递归的终止条件：右孩子为null

//获取二分搜索树的最大值
public E getMaxValue(){
    if(size==0){
        throw new IllegalArgumentException("BST IS empty");
    }
    return getMaxNode(root).e;
}
//获取 以node为根节点，值最大值所在的节点
private BSTNode getMaxNode(BSTNode bstNode){
    if(bstNode.right==null){
        return bstNode;
    }
    return getMaxNode(bstNode.right);
}

最小值

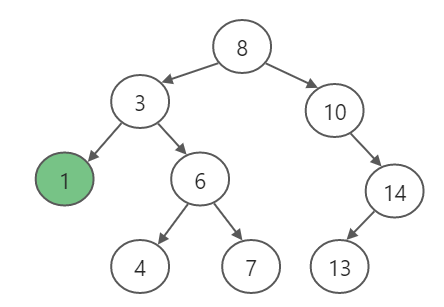
实现思路：

• 递归找左孩子
• 递归的终止条件：左孩子为null

//获取二分搜索树的最小值
public E getMinValue(){
    if(size==0){
        throw new IllegalArgumentException("BST IS empty");
    }
    return getMinNode(root).e;
}
//获取 以node为根节点，值最小值所在的节点
private BSTNode getMinNode(BSTNode bstNode){
    if(bstNode.left==null){
        return bstNode;
    }
    return getMinNode(bstNode.left);
}

2.5插入

思路：这里以插入5为例

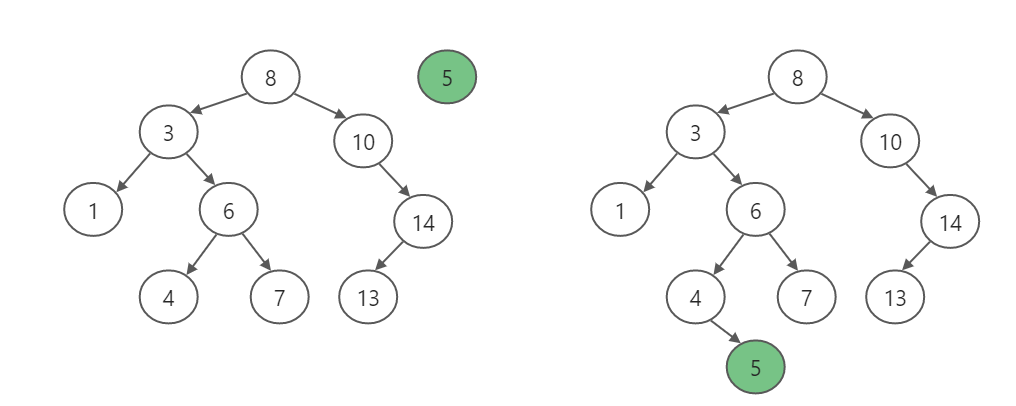
• 5和根节点8比较，比5小，则从8的左孩子开始找
• 5和3比较，比3大，则从3的右孩子开始找
• 5和6比较，比6小，则从6的左孩子开始找
• 5和4比较，比4大，则从4的有孩子开始找
• 此时4的右孩子为空，则找到了5的位置

public void add(E e) {
    root = add(root, e);
}

//以node为根节点，插入e 的递归写法
//返回插入新节点后二分搜索的根
public BSTNode add(BSTNode node, E e) {
    if (node == null) {
        size++;
        return new BSTNode(e);
    }
    if (e.compareTo(node.e) < 0) {
        node.left = add(node.left, e);
    }
    if (e.compareTo(node.e) > 0) {
        node.right = add(node.right, e);
    }
    return node;
}

2.6删除

删除节点，主要有三种情况

• 被删除的节点，没有孩子，则直接删除即可

• 被删除的节点，只有一个孩子，删除后，让孩子顶替自己的位置。
  • 例如（删除最大值，最小值，肯定在情况1和2中）

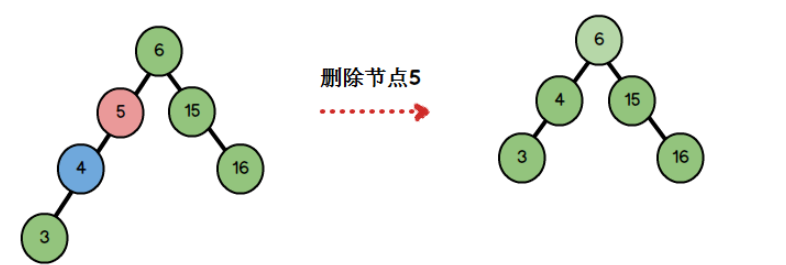
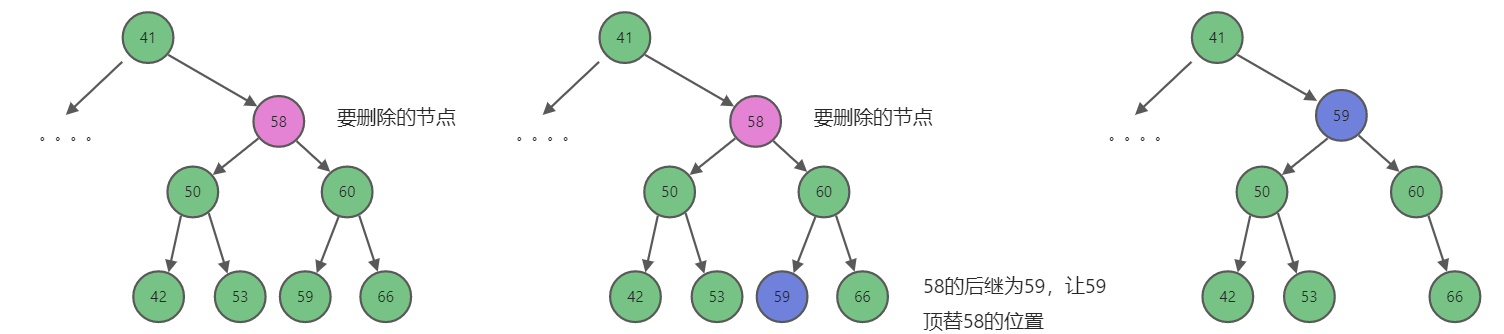
• 被删除的节点，有两个孩子，删除后，让后继节点顶替自己的位置。
  • 通俗点讲：后继为删除节点的右子树中的最小节点

2.6.1删除最小值

//删除二分搜索树的最小值 返回最小值
public E removeMinValue(){
    E e = getMinValue();//获取最小值
    root = removeMinNode(root);
    return e;
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private BSTNode removeMinNode(BSTNode node){
    if(node.left==null){//递归的最终状态，如果node的左孩子为空，则说明它是最小的
        BSTNode temp = node.right;//维护节点的右孩子
        node.right=null;
        size--;
        return temp;//删除后，根节点为右孩子，返回右孩子即可
    }
    //左孩子不为空，说明还不是最小，递归以左孩子为根节点找
    node.left =removeMinNode(node.left);
    return node;
}

2.6.2删除最大值

//删除二分搜索树的最大值，返回最大值
public E removeMaxValue(){
    E e = getMaxValue();
    root = removeMaxNode(root);
    return e;
}

// 删除掉以node为根的二分搜索树中的最大节点
// 返回删除节点后新的二分搜索树的根
public BSTNode removeMaxNode(BSTNode node){
    if(node.right==null){
        BSTNode temp = node.left;
        node.left = null;
        size--;
        return temp;
    }
    node.right = removeMaxNode(node.right);
    return node;
}

2.6.3删除任意节点

//从二分搜索树中删除元素为e的节点
public void remove(E e){
    root =  removeNode(root,e);
}
// 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
private BSTNode removeNode(BSTNode node,E e){
    if(node==null){
        return null;
    }
    if(e.compareTo(node.e)>0){//如果e> node.e 则去node的右孩子找
        node.right =  removeNode(node.right,e);
        return node;
    }else if(e.compareTo(node.e)<0){//如果e< node.e 则去node的左孩子找
        node.left =  removeNode(node.left,e);
        return node;
    }else {//相等 进行删除逻辑
        if(node.left==null){//如果node.left 为空，则逻辑相当于删除 最小节点
            BSTNode temp = node.right;
            node.right = null;
            size--;
            return temp;
        }
        if(node.right==null){//如果node.right 为空，则逻辑相当于删除 最大节点
            BSTNode temp = node.left;
            node.left = null;
            size--;
            return temp;
        }
        //如果左右孩子都不为空，则默认把node的后继放到自己的位置
        //即，找node右孩子的最小节点
        BSTNode rightMin = getMinNode(node.right);
        //且node的后继的右孩子为 removeMinNode(node.right) 这步相当于，把后继节点直接放到node的位置，原来的后继位置删除了
        rightMin.right = removeMinNode(node.right);//注意removeMinNode里面已经有size--方法了
        rightMin.left = node.left;
        node.left = node.right = null;
        return rightMin;
    }
}

代码

public class BSTree <E extends Comparable<E>>{

    class BSTNode{
        private BSTNode left; //左孩子
        private BSTNode right; //右孩子
        private E e; //值

        public BSTNode(E e){
            left = null;
            right = null;
            this.e = e;
        }
    }

    private BSTNode root;
    private int size;

    public int size(){
        return size;
    }

    //判断是否有元素e
    public boolean contains(E e){
        return contains(root,e);
    }

    //判断以node为根节点的二分搜索树，是否有e
    private boolean contains(BSTNode node, E e) {
        if (node == null) {
            return false;
        }
        if (e.compareTo(node.e) == 0) {
            return true;
        } else if (e.compareTo(node.e) > 0) {
            return contains(node.right, e);
        } else {
            return contains(node.left, e);
        }
    }


    public void add(E e) {
        root = add(root, e);
    }

    //以node为根节点，插入e 的递归写法
    //返回插入新节点后二分搜索的根
    public BSTNode add(BSTNode node, E e) {
        if (node == null) {
            size++;
            return new BSTNode(e);
        }
        if (e.compareTo(node.e) < 0) {
            node.left = add(node.left, e);
        }
        if (e.compareTo(node.e) > 0) {
            node.right = add(node.right, e);
        }
        return node;
    }
    //获取二分搜索树的最大值
    public E getMaxValue(){
        if(size==0){
            throw new IllegalArgumentException("BST IS empty");
        }
        return getMaxNode(root).e;
    }
    //获取 以node为根节点，值最大值所在的节点
    private BSTNode getMaxNode(BSTNode bstNode){
        if(bstNode.right==null){
            return bstNode;
        }
        return getMaxNode(bstNode.right);
    }

    //获取二分搜索树的最小值
    public E getMinValue(){
        if(size==0){
            throw new IllegalArgumentException("BST IS empty");
        }
        return getMinNode(root).e;
    }
    //获取 以node为根节点，值最小值所在的节点
    private BSTNode getMinNode(BSTNode bstNode){
        if(bstNode.left==null){
            return bstNode;
        }
        return getMinNode(bstNode.left);
    }

    //删除二分搜索树的最小值 返回最小值
    public E removeMinValue(){
        E e = getMinValue();//获取最小值
        root = removeMinNode(root);
        return e;
    }
    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    private BSTNode removeMinNode(BSTNode node){
        if(node.left==null){//递归的最终状态，如果node的左孩子为空，则说明它是最小的
            BSTNode temp = node.right;//维护节点的右孩子
            node.right=null;
            size--;
            return temp;//删除后，根节点为右孩子，返回右孩子即可
        }
        //左孩子不为空，说明还不是最小，递归以左孩子为根节点找
        node.left =removeMinNode(node.left);
        return node;
    }

    //删除二分搜索树的最大值，返回最大值
    public E removeMaxValue(){
        E e = getMaxValue();
        root = removeMaxNode(root);
        return e;
    }

    // 删除掉以node为根的二分搜索树中的最大节点
    // 返回删除节点后新的二分搜索树的根
    public BSTNode removeMaxNode(BSTNode node){
        if(node.right==null){
            BSTNode temp = node.left;
            node.left = null;
            size--;
            return temp;
        }
        node.right = removeMaxNode(node.right);
        return node;
    }

    //从二分搜索树中删除元素为e的节点
    public void remove(E e){
        root =  removeNode(root,e);
    }
    // 删除掉以node为根的二分搜索树中值为e的节点, 递归算法
    // 返回删除节点后新的二分搜索树的根
    private BSTNode removeNode(BSTNode node,E e){
        if(node==null){
            return null;
        }
        if(e.compareTo(node.e)>0){//如果e> node.e 则去node的右孩子找
            node.right =  removeNode(node.right,e);
            return node;
        }else if(e.compareTo(node.e)<0){//如果e< node.e 则去node的左孩子找
            node.left =  removeNode(node.left,e);
            return node;
        }else {//相等 进行删除逻辑
            if(node.left==null){//如果node.left 为空，则逻辑相当于删除 最小节点
                BSTNode temp = node.right;
                node.right = null;
                size--;
                return temp;
            }
            if(node.right==null){//如果node.right 为空，则逻辑相当于删除 最大节点
                BSTNode temp = node.left;
                node.left = null;
                size--;
                return temp;
            }
            //如果左右孩子都不为空，则默认把node的后继放到自己的位置
            //即，找node右孩子的最小节点
            BSTNode rightMin = getMinNode(node.right);
            //且node的后继的右孩子为 removeMinNode(node.right) 这步相当于，把后继节点直接放到node的位置，原来的后继位置删除了
            rightMin.right = removeMinNode(node.right);//注意removeMinNode里面已经有size--方法了
            rightMin.left = node.left;
            node.left = node.right = null;
            return rightMin;
        }
    }
    //遍历
    //前序遍历
    public void preOrder(){
        preOrder(root);
    }
    public void preOrder(BSTNode node){
        if (node!=null){
            System.out.println(node.e);
            preOrder(node.left);
            preOrder(node.right);
        }
    }

    //中序遍历
    public void inOrder(){
        inOrder(root);
    }
    public void inOrder(BSTNode node){
        if (node!=null){
            inOrder(node.left);
            System.out.println(node.e);
            inOrder(node.right);
        }
    }
    //后续遍历
    public void postOrder(){
        postOrder(root);
    }
    public void postOrder(BSTNode node){
        if (node!=null){
            postOrder(node.left);
            postOrder(node.right);
            System.out.println(node.e);
        }
    }




    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        generateBSTString(root, 0, res);
        return res.toString();
    }

    // 生成以node为根节点，深度为depth的描述二叉树的字符串
    private void generateBSTString(BSTNode node, int depth, StringBuilder res){

        if(node == null){
            res.append(generateDepthString(depth) + "null\n");
            return;
        }

        res.append(generateDepthString(depth) + node.e +"\n");
        generateBSTString(node.left, depth + 1, res);
        generateBSTString(node.right, depth + 1, res);
    }

    private String generateDepthString(int depth){
        StringBuilder res = new StringBuilder();
        for(int i = 0 ; i < depth ; i ++)
            res.append("--");
        return res.toString();
    }
}

参考

• https://class.imooc.com/sale/datastructure?mc_marking=847f8fb5de6faa3343df639065d45b7d&mc_channel=imoocsearch
• http://www.cnblogs.com/skywang12345/p/3561803.html